Shannon információn alapuló többléptékű információtartalom mérési módszer

Az itt bemutatott új matematikai módszer tetszőleges diszkrét mintázat (belső) információtartalmára ad pontosabb becslést Shannon eredeti függvényére építve. A módszert különböző adatsorokon teszteljük és az eredményeket összehasonlítjuk más módszerek eredményeivel.

Abstract: Ebben a tanulmányban egy új többléptékű információtartalom számítási módszert mutatunk be, amely a Shannon-entrópián alapul. A Claude E. Shannon által leírt, és az elemek valószínűségének logaritmusán alapuló eredeti módszer felső korlátot ad a diszkrét mintázatok információtartalmára, de sok esetben (például ismétlődést tartalmazó mintázatok esetén) pontatlan, és nem tükrözi a mintázat valódi információtartalmát. Az itt bemutatott új matematikai módszer tetszőleges diszkrét mintázat (belső) információtartalmára ad pontosabb becslést Shannon eredeti függvényére építve. A módszert különböző adatsorokon teszteljük és az eredményeket összehasonlítjuk más módszerek eredményeivel.

1 Bevezetés

Hagyományosan Shannon információelméletét [13] használták a mintázatok információtartalmának mérésére. A Shannon-információ Claude E. Shannon meghatározása szerint a bizonytalanság vagy meglepetés mértéke, amely egy adott kimenetelhez kapcsolódik a lehetséges kimenetelek halmazában. A Shannon-entrópia, amely a Shannon-információ várható értéke, egy diszkrét mintázat vagy üzenet átlagos információtartalmának számszerűsítésére szolgál. Alapfogalomként szolgál az információelméletben, és széles körben használják kommunikációs rendszerekben és adattömörítésben.

Bizonyos helyzetekben, például ismétlődő mintázatok esetén Shannon eredeti információmérési módszere nem ad kellően pontos eredményt, mert nem veszi figyelembe a mintázatok szerkezetét, csak azok bizonyos statisztikai jellemzőit nézi. Ennek a problémának a megoldására ez a cikk egy új, többléptékű információtartalom számítási módszert mutat be, amely Shannon eredeti elvein alapul. Módszerünk a számítási megközelítés finomításával pontosabb becslést kínál a diszkrét mintázatok belső információtartalmára, függetlenül azok természetétől.

Számos más módszer is létezik a mintázatok információtartalmának mérésére, mint például a Kolmogorov-komplexitás [8], a véletlenszerűség [9] és a tömörítési komplexitás. E módszerek közös tulajdonsága, hogy valamennyien alkalmasak a mintázatok információtartalmának bizonyos pontosságú meghatározására, megértésére, így megfelelő összehasonlítási alapot adnak az újabb módszerek ellenőrzéséhez.

Új módszerünk hatékonyságának ellenőrzésére különféle adatkészletekre alkalmazzuk, és összehasonlítjuk tömörítési algoritmusokkal. Az eredmények azt mutatják, hogy az általunk javasolt Shannon információkon alapuló módszerünk jól közelíti a más módszerekkel mért eredményeket, miközben teljesen más megközelítést alkalmaz.

2 Mintázat

Jelen tanulmányban diszkrét mintázatok belső mennyiségi információtartalmának számításával foglalkozunk. Az információtartalom számítása szempontjából lényegtelen, hogy a mérés tárgya milyen jellegű. Az információtartalmát számíthatjuk eseményeknek, jelforrásokból származó jeleknek, rendszerek állapotának, vagy adatsoroknak, mivel ezek modelljei (véges pontossággal) mind reprezentálhatók diszkrét mintázatként. Egy térbeli mintázaton végighaladva időbeli mintázatot kapunk és fordítva. Ezért nem teszünk különbséget térbeli és időbeli mintázat között. Az alapvető jelölések legyenek a következők.

R

halmazból előállítható véges sorozatok halmazát jelölje

M (R)

\begin{matrix} M (R) = {X : N^{+} \to R} & (1) \end{matrix}

Nevezzük mintázatnak az

X \in M (R)

véges sorozatot:

\begin{matrix} X = [x_{1}, ..., x_{N}] & (2) \end{matrix}

X

sorozat hosszát jelölje:

\begin{matrix} n (X) = N & (3) \end{matrix}

X

sorozat értékkészletének halmazát jelölje:

\begin{matrix} R = {r_{1}, r_{2}, ..., r_{K}} & (4) \end{matrix}

Jelöljük

f (x)

-el az

x \in R_{X}

előfordulásainak számát az

X

sorozatban:

\begin{matrix} f (x) = \sum_{i = 1}^{K} [r_{i} = x] & (5) \end{matrix}

X

mintázat bármely

x \in R

elemének relatív gyakorisága legyen:

\begin{matrix} p (x) = f (x) / N & (6) \end{matrix}

X_{1} X_{2} ... X_{K}

mintázatok konkatenációját jelölje:

\begin{matrix} X_{1} X_{2} ... X_{K} = ∥_{i = 1}^{K} X_{i} & (7) \end{matrix}

3 Információtartalom

Az információtartalom intuitív módon értelmezhető, ha csak az értelmezhető információtartalmat vizsgáljuk [1]. Ebben a tanulmányban a teljes belső információtartalom mennyiségét vizsgáljuk anélkül, hogy értelmeznénk, vagy a kontextust figyelembe vennénk.

Egy mintázat információtartalmát többek között jellemezhetjük a mintázat egyes elemeinek valószínűtlenségével (Shannon-információ [13]), a mintázat legtömörebb leírásának hosszával (Kolmogorov-komplexitás [8]), vagy a mintázat véletlenszerűségének mértékével [9].

Alapvető különbség Shannon és Kolmogorov nézőpontja között, hogy Shannon csak a mintázatot létrehozó véletlenszerű információforrás valószínűségi jellemzőit tekintette, figyelmen kívül hagyva magát a mintázatot. Ezzel szemben Kolmogorov csak magára a mintázatra koncentrált[5]. Kolmogorov és Chaitin definíciójukban azt a mintázatot nevezték (pontatlanul fogalmazva) véletlenszerűnek, amelynek maximális az információtartalma[10].

Az információ, a komplexitás és a véletlenszerűség annyira hasonló tulajdonságokkal rendelkeznek, hogy jogosan feltételezhetjük: lényegében ugyanazt a dolgot közelítik különböző módszerekkel. Elegendő, ha arra gondolunk, hogy az azonos elemekből álló mintázatnak a Shannon-információja, a Kolmogorov-komplexitása és a véletlenszerűsége egyaránt minimális, míg a valódi véletlen mintázat esetén mindhárom érték maximális.

Az entrópia és az információ fogalmát gyakran keverik[3], ezért fontos megemlíteni, hogy az entrópia nem más, mint az elemenkénti átlagos információtartalom, más néven információsűrűség.

Intuitív módon megközelítve az információmennyiség olyan függvény, amelyre teljesülnek az alábbi feltételek:

A nulla hosszúságú vagy azonos elemekből álló mintázat információtartalma nulla.
Az ismétlődő szakaszokból álló mintázat információtartalma (közel) azonos az ismétlődő szakasz információtartalmával.
Egy mintázatnak és a tükörképének azonos az információtartalma.
Diszjunkt értékkészletű mintázatok információtartalmának összege kisebb, mint az összefűzött mintázat információtartalma.
A valódi véletlenszerű mintázatok információtartalma közel maximális.

Az információtartalom legyen az

I

függvény, amely bármely tetszőleges

X \in M (R)

mintázathoz egy nemnegatív valós számot rendel:

\begin{matrix} I : M_{R} \to R^{+} & (8) \end{matrix}

Továbbá teljesülnek az alábbi feltételek:

$I (X) = 0 \leftrightarrow | R_{X} | < 2$
$I (∥_{i = 1}^{K} X) = I (X)$
$I (∥_{i = 1}^{K} X_{i}) = I (∥_{i = K}^{1} X_{i})$
$| \cap_{i = 1}^{K} R_{X_{i}} | = \emptyset \Rightarrow I (∥_{i = 1}^{K} X_{i}) > \sum_{i = 1}^{K} I (X_{i})$
$I (X) \leq I (X_{T R}), \forall X \in M (R), | X | = | X_{T R} |$ esetén, ahol $X_{T R} \in M (R)$ valódi véletlen mintázat.

Mivel bármely mintázat leírható tovább nem bontható bináris alakban, ezért az információtartalom mértékegysége legyen a bit.

Belátható, hogy bármely

X \in M (R)

mintázat esetén, ha

N = n (X)

és

K = | R |

, akkor az

X

maximális információtartalma:

\begin{matrix} I_{M A X} (X) = N \cdot l o g_{2} (K) & (9) \end{matrix}

Vagyis

I (X) \leq I_{M A X} (X)

bármely

X \in M (R)

mintázatra. Bináris mintázat esetén

I_{M A X} (X) = N

, a mintázat hossza, ami azt jelenti, hogy maximum

N

bit információ (döntés) szükséges a mintázat leírásához.

Ha ismerjük a maximális információtartalmat, akkor kiszámítható a relatív információtartalom:

\begin{matrix} I^{(r e l)} (X) = I (X) / I_{M A X} (X) & (10) \end{matrix}

4 Shannon-információ

A Kolmogorov-komplexitás elméletben ugyan jobb közelítést adna a mintázatok információtartalmára, de bizonyítottan nem kiszámítható[5], ellentétben a Shannon-információval [13], amely hatékonyan számítható, de kevésbé jól közelíti a tényleges információtartalmat. A Shannon-információ a mintázat információtartalmát a mintázat elemeinek a várható előfordulási valószínűsége (relatív gyakorisága) alapján számítja.

Egy tetszőleges

X \in M (R)

mintázat Shannon-információja:

\begin{matrix} I_{S} (X) = \sum_{i = 1}^{N} l o g_{2} (\frac{1}{p (x_{i})})) & (11) \end{matrix}

Mivel a mintázat elemeinek a relatív gyakorisága (várható előfordulása) csak egy statisztikai jellemzője a mintázatnak (a sok közül), és nem veszi figyelembe az elemek sorrendjét, ezért a Shannon-információ gyakran nagyon pontatlan becslést ad az információtartalomra. A Shannon-információ értéke megegyezik minden olyan azonos hosszúságú mintázat esetén amelyek elemei azonos relatív gyakoriságúak. Ha

X \in M (R)

Y \in M (Q)

és

| R | = | Q | = K

akkor teljesül, hogy:

\begin{matrix} I_{S} (X) = I_{S} (Y), h a {p (r_{1}), p (r_{2}), ..., (r_{K})} = {p (q_{1}), p (q_{2}), ..., (q_{K})} & (12) \end{matrix}

A Shannon-információ figyelmen kívül hagyja a mintázatok különböző léptékű struktúráját, az abban kódolt törvényszerűségeket, így az ismétlődő szakaszokból álló mintázatok információtartalmát is túlbecsüli.

A probléma egy egyszerű példával szemléltethető. Számoljuk ki a következő három mintázat Shannon-entrópiáját:

$X_{A} : 001101101010111001110010001001000100001000010000$
$X_{B} : 101010101010101010101010101010101010101010101010$
$X_{C} : 111111110000000011111111000000001111111100000000$

Az értékkészlet mindhárom esetben

R = 0, 1

, az egyes elemek valószínűsége

p (0) = 0.5

és

p (1) = 0.5

, a Shannon-entrópia pedig

I_{S} (X) = \sum_{i = 1}^{N} l o g_{2} (\frac{1}{p (x_{i})}) = 16 b i t

, pedig nyilvánvaló, hogy az adatsorok információtartalma jelentős mértékben eltér egymástól. Az

X_{A}

adatsor információtartalma a véletlenszerűségéből adódóan közel 16 bit, míg a másik két adatsor információtartalma jóval kisebb, hiszen ismétlődő szakaszokat tartalmaznak. Az

X_{B}

adatsorban például a 2 bites

[10]

szakasz ismétlődik, ami azt jelenti, hogy az információtartalma a 2 bithez áll közelebb.

A probléma az, hogy fenti példában az adatsorokat elemi szinten vizsgáljuk, és a Shannon-entrópiafüggvényünk nem vesz tudomást az adatsor nagyobb léptékű szerkezetéről, mint például az 1 jelnél hosszabb, ismétlődő szakaszok jelenléte. Ezért kézenfekvő az olyan módszerek kidolgozása, amely a Shannon-entrópián alapulnak, de az adatsorokat a felbontás teljes spektrumában, a teljes frekvenciatartományban elemzik, és így pontosabb közelítést adnak az adatsor információtartalmára. Számtalan ilyen megoldást publikáltak már, amelyek például a [2] és a [6] cikkekben olvashatóak. Jelen cikk további módszereket mutat be.

5 SSM-információ

5.1 Shannon-információspektrum

Legyen az

X

mintázat

r

hosszúságú szakaszonkénti partícionálása, ha

m = [N / r]

\begin{matrix} X^{(r)} = [x_{1} ... x_{r}, x_{r + 1} ... x_{2 r}, ..., x_{(m - 1) \cdot r + 1} ... x_{m \cdot r}] & (13) \end{matrix}

A következő sorozatot nevezzük az

X

mintázat Shannon-információspektrumának (SP, Shannon Information Spectrum):

\begin{matrix} I_{S P}^{(r)} (X) = I_{S} (X^{(r)}), r = 1, ..., [N / 2] & (14) \end{matrix}

X^{(r)}

sorozatokból kihagyjuk az

r

-nél rövidebb (csonka) partíciókat, azokat, amelyek rövidebbek

r

-nél. Az

r > [N / 2]

esetekben az

I_{S P} (X^{(r)}) = 0

lenne, ezért ezeket szintén kihagyjuk a spektrumból.

image: images/blog/publikaciok/tobblepteku_informaciomeres/0_media_PROJECTS_Publik__ci__k_2023_-_Shannon_i_____ci__tartalom_m__r__si_m__dszer_K__pek_ISP.png

1. Ábra. Az $A$ diagramon az $X_{A}$ véletlenszerű mintázat Shannon-információspektruma látható, a $B$ ábrán pedig az $X_{C}$ ismétlődő mintázaté (I. függelék). Látható, hogy a $B$ esetben bizonyos frekvenciákon alacsonyabb érték jelenik meg.

5.2 Maximális Shannon-információspektrum

Az Shannon-információspektrum a véletlenszerű adatsorok esetén lesz maximális, amit nevezzünk maximális Shannon-információspektrumnak (SMS, Shannon Maximum Information Spectrum) és a következő képlettel számítjuk:

\begin{matrix} I_{S M S}^{(r)} (X) = m \cdot l o g_{2} (m i n (K^{r}, m)), r = 1, ..., [N / 2] & (15) \end{matrix}

r

elég kicsi, akkor az

X^{(r)}

sorozatban nagy valószínűséggel minden lehetséges érték szerepel, ezért a mért információmennyiség közelítőleg meg fog egyezni a mintázat maximális lehetséges információtartalmával, azaz ha

r

kicsi, akkor

I_{S P M}^{(r)} (X^{(r)}) \approx I_{M A X} (X^{(r)}) = N \cdot l o g_{2} (n)

image: images/blog/publikaciok/tobblepteku_informaciomeres/1_media_PROJECTS_Publik__ci__k_2023_-_Shannon_i___artalom_m__r__si_m__dszer_K__pek_ISMS_-_ISP.png

2. Ábra. A maximális Shannon-információspektrum (ISMS) és az $X_{C}$ ismétlődő mintázat Shannon-információspektrumának (ISP) az összehasonlítása.

5.3 Normalizált Shannon-információspektrum

Ha arra vagyunk kíváncsiak, hogy a maximális értékhez képest relatíve mennyinek látszik az információtartalom az egyes felbontásokban, akkor a spektrumot a maximális spektrummal normalizálhatjuk a

[0 - N \cdot l o g_{2} (n)]

tartományba. A normalizált Shannon-információspektrum (SNS, Shannon Normalized Information Spectrum) legyen a következő sorozat:

\begin{matrix} I_{S N S}^{(r)} (X) = {\begin{matrix} \frac{I_{S P}^{(r)} (X)}{I_{S M S}^{(r)} (X)} \cdot I_{M A X} (X), & i f | R_{X^{(r)}} | > 1 \\ r \cdot \frac{I_{S P}^{(1)} (X)}{N}, & i f | R_{X^{(r)}} | = 1 \end{matrix} w h e r e r = 1, ..., [N / 2] & (16) \end{matrix}

Abban az esetben, ha a normalizált érték

0

lenne, az azt jelenti, hogy ismétlődő partíciókról van szó. Ebben az esetben az információtartalom az ismétlődő partíció információtartalma lesz, és az elemi felbontás egy elemének átlagos Shannon-entrópiáját megszorozzuk a partíció hosszával:

r \cdot \frac{I_{S P}^{(1)} (X)}{N}

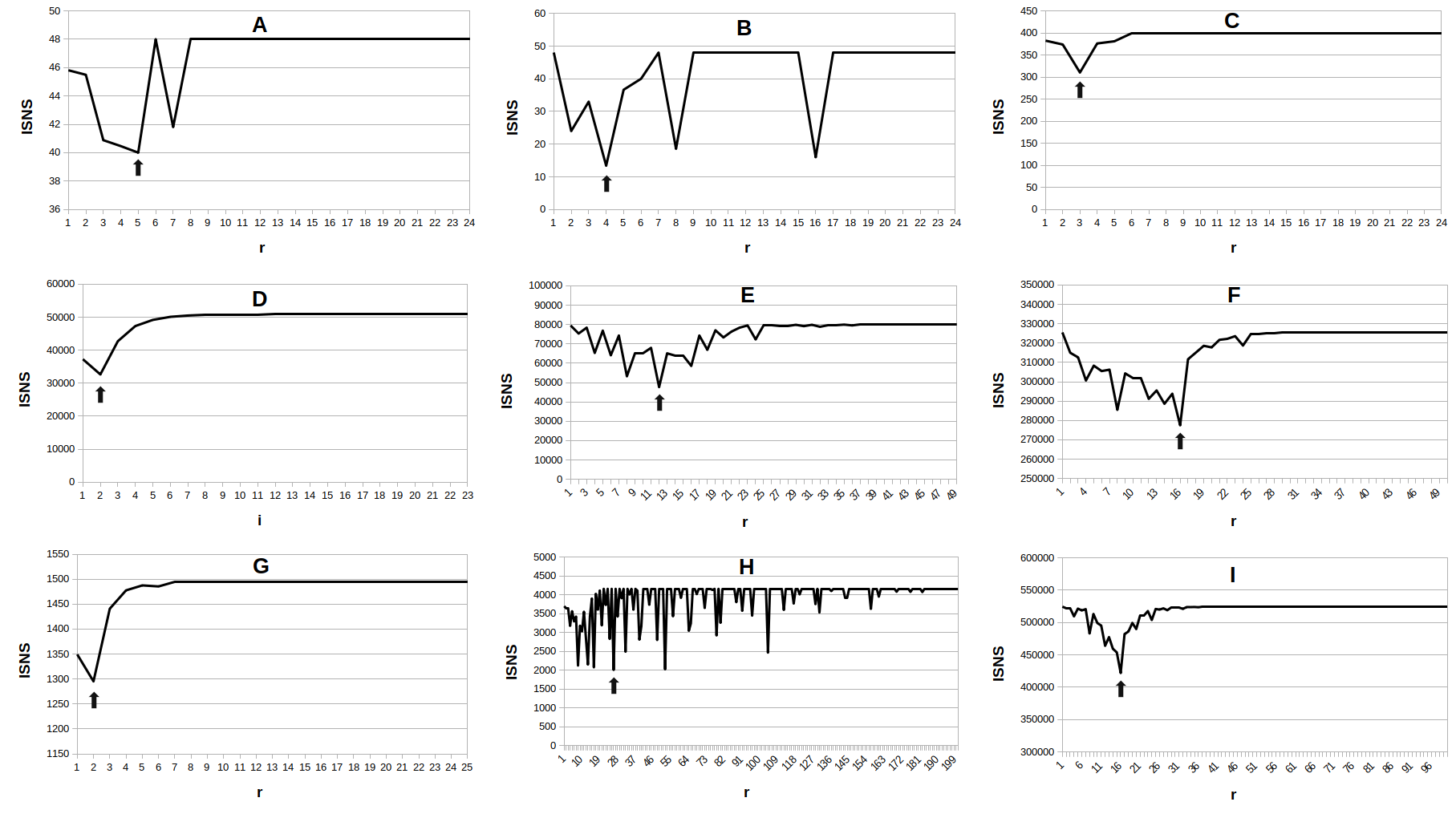
image: images/blog/publikaciok/tobblepteku_informaciomeres/2_media_PROJECTS_Publik__ci__k_2023_-_Shannon_i____ci__tartalom_m__r__si_m__dszer_K__pek_ISNS.png

3. Ábra. Nagyon különböző forrásokból származó mintázatok normalizált Shannon-információspektrumainak összehasonlítása. Látszik, hogy a különböző mintázatoknak mennyire eltérő a spektruma, de a legtöbb esetben van olyan felbontás, ahol határozott minimumot mutat az információtartalom. A minimumokat nyíllal jelöltük. A: random bináris mintázat, B: bináris mintázat ismétlődő szakaszokkal, C: DNS-szakasz, D: angol szöveg, E: ECG-jel, F: beszédet tartalmazó hangfelvétel, G: a napfoltok számának alakulása 1700-2021 között, H: szeizmogram, I: Lena fotója.

5.4 SSM-információ

Tudjuk, hogy a Shannon-információ minden esetben felső becslést ad, ezért a normalizált spektrumból akkor kapjuk meg az információtartalom legpontosabb közelítését, ha a minimumát vesszük. A normalizált spektrumból számított információtartalmat nevezzük SSM-információnak (Shannon Spectrum Minimum Information):

\begin{matrix} I_{S S M} (X) = {m i n}_{i = 1}^{[} (I_{S N S}^{(i)} (X)) & (17) \end{matrix}

Különböző mintázatok (I. függelék) Shannon-információja, SSM-információja és tömörítési komplexitása bit-ben kifejezve:

Mintázat	Forrás	$I_{M A X} (X)$	$I_{S} (X)$	$I_{S S M} (X)$	$I_{Z I P} (X)$	$I_{7 Z} (X)$	$I_{Z P A Q} (X)$
X $_{A}$	Véletlenszerű bináris mintázat.	48	46	40
X $_{B}$	Ismétlődő bináris mintázat.	48	48	2
X $_{C}$	Ismétlődő bináris mintázat.	48	48	13
X $_{D}$	Ismétlődő szövegrész.	362	343	58
X $_{E}$	Ismétlődő szövegrész egy karakternyi hibával.	374	347	116
X $_{F}$	Véletlenszerű DNS mintázat.	471	422	409
X $_{G}$	COVID vírus DNS-szakasza.	471	405	388
X $_{H}$	Véletlenszerű karaktersorozat (0-9, a-z, A-Z).	1209	1174	1174
X $_{I}$	Angol szöveg (James Herriot's Cat Stories).	1104	971	971
X $_{J}$	Naptevékenység 1700-2021 között (A-Z).	1495	1349	1295
X $_{K}$	Isaac Asimov: True love.	50901	37266	32649	30904	29968	25248
X $_{L}$	Bináris ECG szignál.	80000	79491	47646	52320	41032	36968
X $_{M}$	Bináris földmozgás adat.	313664	312320	171546	83920	66064	45824
X $_{N}$	Beszéd hangfelvétel.	325472	325342	277489	286760	257856	251408
X $_{O}$	Lena képe.	524288	524216	422085	443096	371360	337408

Különböző mintázatok (I. függelék) relatív Shannon-információja, SSM-információja és tömörítési komplexitása a maximális információhoz viszonyítva:

Mintázat	Forrás	$I_{S}^{(r e l)} (X)$ %	$I_{S S M}^{(r e l)} (X)$ %	$I_{Z I P}^{(r e l)} (X)$ %	$I_{7 Z}^{(r e l)} (X)$ %	$I^{(r e l)}_{Z P A Q} (X)$ %
X $_{K}$	Isaac Asimov: True love.	73	64	61	59	50
X $_{L}$	Bináris ECG szignál.	99	60	65	51	46
X $_{M}$	Bináris földmozgás adat.	100	55	27	21	15
X $_{N}$	Beszéd hangfelvétel.	100	85	88	79	77
X $_{O}$	Lena képe.	100	81	85	71	64

A táblázatból látszik, hogy az SSM-információ hasonló eredményeket ad, mint a tömörítési algoritmusok. Általánosságban igaz, hogy minél nagyobb számítási igényű egy tömörítési vagy információ-mérő eljárás, annál jobban közelíti a Kolmogorov-komplexitást. A vizsgált példákban az SSM-információ eredményei általában a ZIP és a 7Z eredményei között helyezkednek el, így az SSM-információ számítási komplexitásának is hasonlónak kell lennie a ZIP és a 7Z számítási komplexitásához.

image: images/blog/publikaciok/tobblepteku_informaciomeres/3_media_PROJECTS_Publik__ci__k_2023_-_Shannon_i___talom_m__r__si_m__dszer_K__pek_IS_ISSM_ZPAQ.png

3. Ábra. A különböző információmérési módszerek eredményeinek összehasonlítása.

image: images/blog/publikaciok/tobblepteku_informaciomeres/4_media_PROJECTS_Publik__ci__k_2023_-_Shannon_i____r__si_m__dszer_K__pek_ISSM_ZIP_7Z_ZPAQ_AVR.png

4. Ábra. A különböző információmérési módszerek átlagos eredményeinek összehasonlítása.

5.5 Számítási komplexitás összehasonlítása

Ha nem ismerjük a jelsorozat jelkészletét, az első lépés, hogy meghatározzuk a jelsorozatban előforduló jelek számát, ami

O (N \cdot l o g N)

asszimptotikus komplexitású.

A Shannon-információ meghatározása két lépésből áll. Az első lépésben meghatározzuk a jelek gyakoriságát, ami

O (N)

komplexitású, második lépésben pedig összegezzük az egyes jelek entrópiáját, így a Shannon-információ összkomplexitása

O (N \cdot l o g N) + O (N) = O (N \cdot l o g N)

A tömörítési komplexitás számítására használt ZIP, 7Z és ZPAQ algoritmusok esetén a komplexitás általában

O (N)

és

O (N \cdot l o g N)

között van, de a ZPAQ esetén lehet ennél nagyobb [7] [12] [11].

Az SSM-információ esetén az első lépés szintén a jelek gyakoriságának meghatározása, ami

O (N)

komplexitású. A második lépésben a Shannon-információspektrum kiszámítása

O (N) + O (N / 2) + O (N / 3) + ... + O (2) = O (N \cdot l o g N)

komplexitású, végül a spektrum minimuma meghatározható

O (N)

komplexitással. Az SSM-információ kiszámításának komplexitása legrosszabb esetben

O (I_{S S M} (X)) = O (N \cdot l o g N) + O (N) + O (N \cdot l o g N) + O (N) = O (N \cdot l o g N)

, ami a tömörítési algoritmusokéval azonos.

5.6 Ismert problémák

Minden információmennyiség számítási módszernek vannak pontatlanságai. Az SSM-információ egyik problémája, hogy ha egy ismétlődő mintázatban nem tökéletes az ismétlődés, az SSM-információ értéke nagyobb a vártnál, amint az alábbi példa is mutatja.

$X$	$I_{S S M} (X)$ [bit]
123456789 123456789 123456789	29
223456789 123456789 123456789	50

6 Konklúzió

Az SSM információ a tömörítési komplexitásokkal összemérhető pontossággal képes meghatározni a mintázatok információtartalmát, ugyanakkor egyszerű. Az itt bemutatott információspektrum egy hasznos vizuális eszközt biztosít a mintázatok információszerkezetének tanulányozására.

References

Scoville, John, "Fast Autocorrelated Context Models for Data Compression", (2013).
Laszlo Lovasz, Complexity of Algorithms (Boston University, 2020).
Ben-Naim, Arieh, "Entropy and Information Theory: Uses and Misuses", Entropy (2019).
Pieter Adriaans, "Facticity as the amount of self-descriptive information in a data set", (2012).
Juha Karkkainen, "Fast BWT in small space by blockwise suffix sorting", Theoretical Computer Science (2007).
A. N. Kolmogorov, "On tables of random numbers", Mathematical Reviews (1963).
Laszlo Lovasz, "Information and Complexity (How To Measure Them?)", The Emergence of Complexity in Mathematics, Physics, Chemistry and Biology, Pontifical Academy of Sciences (1996).
Anne Humeau-Heurtier, "The Multiscale Entropy Algorithm and Its Variants: A Review", Entropy (2015).
Allen, Benjamin and Stacey, Blake and Bar-Yam, Yaneer, "Multiscale Information Theory and the Marginal Utility of Information", Entropy (2017).
Goldberger, A. and Amaral, L. and Glass, L. and Hausdorff, J. and Ivanov, P. C. and Mark, R. and Stanley, H. E., "PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals.", Circulation (2000).
Markus Mauer, Timo Beller, Enno Ohlebush, "A Lempel-Ziv-style Compression Method for Repetitive Texts", (2017).
Grunwald, Peter and Vitanyi, Paul, "Shannon Information and Kolmogorov Complexity", CoRR (2004).
Claude E. Shannon, "A Mathematical Theory of Communication", Bell System Technical Journal (1948).
Ervin Laszlo, Introduction to Systems Philosophy (Routledge, 1972).
Olimpia Lombardi and Federico Holik and Leonardo Vanni, "What is Shannon information?", Synthese (2015).

Függelék

I. Példa mintázatok

Jelölés	Mintázat vagy annak részlete	Hossz	Magyarázat
$X_{A}$	001101101010111001110010001001000100001000010000	48 bit	Véletlenszerű bináris mintázat.
$X_{B}$	101010101010101010101010101010101010101010101010	48 bit	Ismétlődő bináris mintázat.
$X_{C}$	111111110000000011111111000000001111111100000000	48 bit	Ismétlődő bináris mintázat.
$X_{D}$	The sky is blue. The sky is blue. The sky is blue.	101 karakter	Ismétlődő szövegrész.
$X_{D}$	The sky is blue. The sky is blue. The sky is blue.	101 karakter	Ismétlődő szövegrész.
$X_{E}$	The sky is blue. The sky is blue. The sky is blue.	101 karakter	Ismétlődő szövegrész egy karakternyi hibával.
$X_{E}$	The sky is blue. The sky is glue. The sky is blue.	101 karakter	Ismétlődő szövegrész egy karakternyi hibával.
$X_{F}$	cagtttctagctatattagcgggcacgactccactgcgcctatgcggaag	200 karakter	Véletlenszerű DNS mintázat.
	cttgatcaaattttgaccagatcttaggtaacctgaacaagtcagttcgt
	aggcgtcgattggccgacgggtgcgaagaaaaaagtgatcgttgtccaac
	atctctagtacccaccgttgtgatgtacgttatacggacacgagcatatt
$X_{G}$	cggcagtgaggacaatcagacaactactattcaaacaattgttgaggttc	200 karakter	COVID vírus DNS-szakasza.
	aacctcaattagagatggaacttacaccagttgttcagactattgaagtg
	aatagttttagtggttatttaaaacttactgacaatgtatacattaaaaa
	tgcagacattgtggaagaagctaaaaaggtaaaaccaacagtggttgtta
$X_{H}$	EK8Pi5sv2npTfzoaMNp87QtT5kbIUQkTJzHwICCstSmg4aksHT	200 karakter	Véletlenszerű karaktersorozat (0-9, a-z, A-Z).
	MwztgHFg3j8AoIobN3FycCLidGeyROiNyG5itB9kxyez1LZjFF
	HIBjipE7hidZyiJmilXM0mwnxzlzWSfQ0xP1OuFpWosMwS1cjY
	t4nyv4ONx1FceWkAf8SdvDGZVzeVzq2EmOqRF6Im2iudcYRswj
$X_{I}$	I think it was the beginning of Mrs. Bond's	221 karakter	Angol szöveg (James Herriot's Cat Stories)
	unquestioning faith in me when she saw me
	quickly enveloping the cat till all you could
	see of him was a small black and white head
	protruding from an immovable cocoon of cloth.
$X_{J}$	ABCDFIEDBBAAAABEHJJGEEDBDGMSPLHFBACFKMRPLGDCA[...]	321 karakter	Naptevékenység 1700-2021 között (A-Z).
$X_{K}$	My name is Joe. That is what my colleague,	8391 karakter	Isaac Asimov: True love.
	Milton Davidson, calls me. He is a programmer and
	I am a computer program. [...]
$X_{L}$	1011000100110011101110111011001100110011[...]	80000 bit	Bináris ECG szignál [4].
$X_{M}$	110000101000000011000010100000001100001010000[...]	313664 bit	Bináris földmozgás adat.
$X_{N}$	0101001001001001010001100100011011100100[...]	325472 bit	Beszéd hangfelvétel.
$X_{O}$	1010001010100001101000001010001010100011[...]	524288 bit	Lena fotója (256x256 pixel, szürkeárnyalatos).

Szerző:

Pőcze Zsolt

Volgyerdo Nonprofit Kft., Nagybakonak, HUN, 2023

Ma	185
Tegnap	203
Ezen a héten	185
Ebben a hónapban	1847
Összesen	699705